Shattering
How does a gas cloud cool? The common picture is that it does so first isochorically, i.e., with a change of temperature but essentially no change of the shape of the gas cloud. This would mean that then the cloud is wildly out of pressure balance.
McCourt et al. (2018), however, conjectured in arXiv:1610.01164
that instead, the cloud breaks up while cooling into a lot of small droplets of size $\mathrm{min}(c_{\mathrm{s}}t_{\mathrm{cool}}) \sim 0.1 (n / 1\,\mathrm{cm}^3)^{-1}\,$ (here $n$ is the gas number density).
They call this process “shattering” and explain in their paper how it can explain a wide range of observations.
The major idea of McCourt et al. (2018) is based on a timescale argument. If a cloud of gas cools to a new temperature $T$ this occurs on a short timescale $t_{\mathrm{cool}}$.
On the other hand, the time it takes for the pressure to equilibrate via contraction of a system of size $r$ is of order the sound crossing time $r / c_{\mathrm{s}}$. Thus, if the cloud is large, it might be out of pressure balance a long time. Instead, they proposes that the gas cloud will fragment in smaller pieces of size $c_{\mathrm{s}} t_{\mathrm{cool}}$. If those clouds were to cool further, a fragmentation cascade follows until the cloudlets are of size $\mathrm{min}(c_{\mathrm{s}}t_{\mathrm{cool}})$ from which point onward the sound crossing is smaller than the cooling time, thus, the pressure can equilibrate quickly.
In arXiv:1912.07808 , we wanted to revisit the “shattering” process, mainly to address the question under which conditions it occurs. Specifically, does it occur in three-dimensions and whether a large (non-linear) initial overdensity is required – which does not exist in the context of, e.g., precipitation.
This is a video of a gas cloud cooling from $\sim 10^5$K to $\sim 10^4$K, and clearly “shattering”:
Note that this simulation has been run in 3D using the ATHENA code.
As explained above, the shattering process only happens for large enough clouds, i.e., if $r_{\rm cl} \gg l_{\rm shatter}$ where we defined the shattering length scale $l_{\rm shatter} \equiv \mathrm{min}(c_{\mathrm{s}} t_{\mathrm{cool}})$.
This shows a smaller cloud roughly the size $l_{\rm shatter}$ undergoing the same cooling process:
The pressure slices of these two simulations are:
and
Can you guess which was the shattered one?
Interestingly, the size is not the only parameter which decides whether a cloud shatters or not…but also how “far” it is cooling. The videos above are of simulations cooling from $\sim 10^5$K to $\sim 10^4$K, i.e., by a factor of $10$. This is a simulation of a cloud much larger than $l_{\rm shatter}$d` but cooling only by a factor of $1.5$:
Is pulsates and does not break apart! The pulsations is due to the fact that the pressure overshoots inside the cloud leading to another expansion, and the reason that it didn’t break up is that is has not been perturbed enough out of pressure balance.
Here are the three cases summed up in one figure:
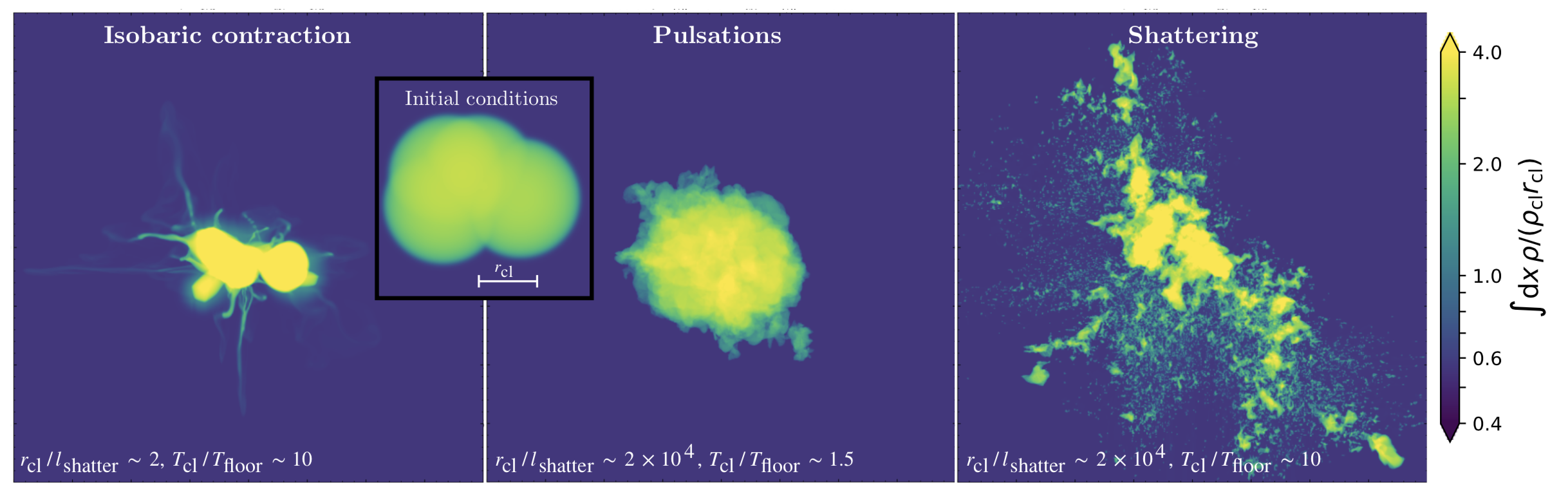
The threshold whether a cloud shatters, i.e., what factor $T_{\rm cl} / T_{\rm floor}$ is required for a large cloud to shatter depends, on the initial overdensity. In fact, we found this relation to be linear (with a small dependence on redshift) which means that clouds with a final overdensity of $\chi_{\rm f} = \chi_{\rm i} T_{\rm cl} / T_{\rm floor} > \chi_{\rm crit} \sim 300$ will shatter.
The reason for this is essentially a competition between the violent “explosion” we’ve seen above, and the re-gathering of droplets.
See for instance a videos with $\chi_{\rm i}= 10$ and $T_{\rm cl} / T_{\rm floor} = 20$, i.e., $\chi_{\rm f}=200$
Here, the droplets regather quickly into larger clouds.
Compare this to a simulation where also $\chi_{\rm i}= 10$ but $T_{\rm cl} / T_{\rm floor} = 40$, i.e., $\chi_{\rm f}=400$
In this case, the coagulation process is not as quick, leaving a “mist” of droplets. Read more details in arXiv:1912.07808 .