Cloud crushing
Both absorption and emission line studies of galaxies show that cold gas around them is commonly ouflowing at speeds of ∼several hundred km/s (see review by Veilleux et al., 2005, and references therein). This robust observational fact poses a severe challenge to our theoretical models of galaxy formation since (i) most feedback mechanisms (e.g., supernovae feedback) accelerate hot gas, and (ii) the timescale it takes to accelerate a blob of cold gas via a hot wind is roughly an order of magnitude larger than the time it takes to destroy the blob (of order the Kevin-Helmholtz and Rayleigh-Taylor timescale of the problem and usually denoted the ‘cloud crushing time’ tcc). Specifically, simple analytic estimates of an adiabatic gas cloud being pushed by a wind yield the ratio of the two timescales to be ∼ χ^1/2 (Klein et al., 1994). Here, χ is the density contrast between the cold and the hot gas which typically takes values of ∼ 100 − 1000 in galactic environments. This result has since then been backed up by several numerical studies which show that cold gas cannot be entrained in the hot wind but instead mixes into the hot gas and heats up.
This is also shown in the video below where we can see that the clump of dense gas gets destroyed on a timescale of a few tcc:
Recently, Zhang et al. (2017) summarized this discrepancy between observations and theory by using hydrodynamical results in the literature combined with an analytic formulation for the outflows which allowed them to derive theoretically feasible outflow speeds of cold gas. They compare their findings to observations, and concluded that hot winds cannot accelerate the cold gas to the observed velocities, or – as their title “Entrainment in Trouble” suggests.
In arXiv:1806.02728 we re-visited this problem using Athena simulations with a similar setup to previous simulations which included radiative cooling. Our results mostly confirm the previous findings, that is, show that cooling is commonly not efficient enough the prevent the destruction of cold gas. However, we also identify some region of parameter space where the cooling efficiency of the mixed, ‘warm’ gas is large enough where not only the cold gas does not get destroyed but instead seeds additional cooling in the ambient medium, leading to a formation of new, comoving cold gas which can exceed the original cold gas mass.
This can be seen in this video below where we see new, cold gas formation in the tail of the cloud.
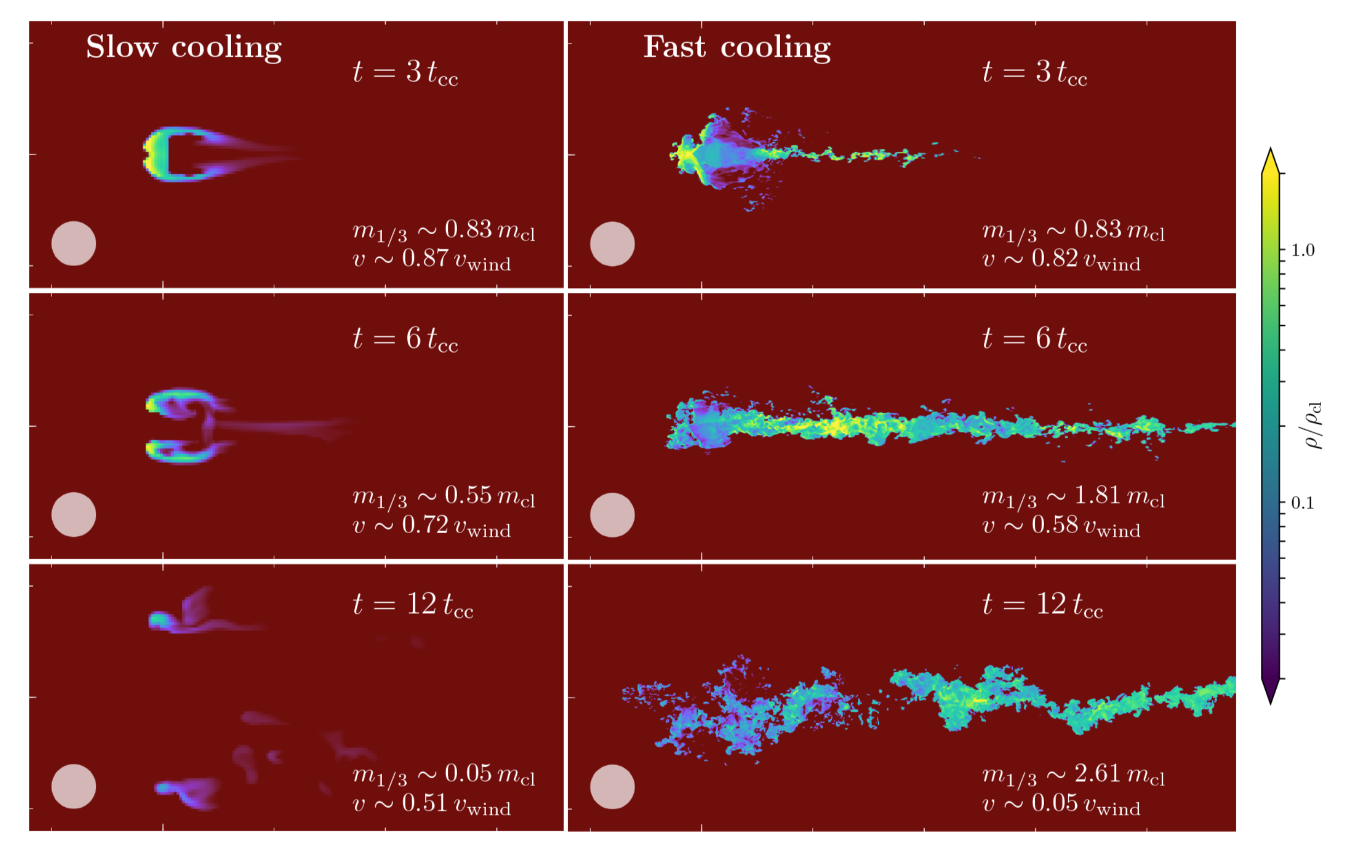
The main result of our first paper on this subject was that we identified the criterion t_{cool, mix} / t_cc < 1. If fulfilled, the cloud survives and can get entrained by the hot wind. The figure below shows visually what happens if this criterion is fulfilled (right panels) and if t_{cool, mix} / t_cc > 1 (left panels).
In follow up work we found that this hold under various conditions, e.g., also if magnetic fields are added. Here is a video of the density projection with strong magnetic fields (plasma beta of both the cloud and the wind of order unity):
Note how the morphology is quite different to the pure hydro case?
Also, note how in both the hydro and the MHD simulations the cold gas cloud keeps on growing even once the cloud is entrained. This is maybe counter-intuitive: one might expect that the mass growth is proportional to the shear since this increases mixing and, thus, cooling. However, in arXiv:1907.04771 we studied the mass growth more closely and found that it is cooling induced which implies that the cold gas keeps on growing even once the cloud is fully entrained.
This opens up a range of possibly implications for this process. For instance, we know that quite a lot of cold gas can be found around galaxies (often referred to as the `circumgalactic medium’). This process might be responsible for this cold gas (which we also discuss in arXiv:1907.04771 ).
More videos
Parameters:
-
- r = rcl / dcell, i.e., describes the resolution
- χ is the initial overdensity of the clump
Hydrodynamics only
r=64, χ = 100, tcool,mix/tcc ~ 0.08
r=8, χ = 100, tcool,mix/tcc ~ 8
r=64, χ = 10, tcool,mix/tcc ~ 0.08
r=8, χ = 1000, tcool,mix/tcc ~ 0.05
r=32, χ = 100, M = 3, tcool,mix/tcc ~ 0.08
r=16, χ = 100, tcool,mix/tcc ~ 0.08, bcl ~ bwind ~ 1
With MHD where the plasma beta parameter of the cloud and the wind are unity.
And the magnetic field: